Tomoyuki ICHIBA
Professor, Department of Statistics & Applied Probability and Center for Financial Mathematics and Actuarial Research
at University of California Santa Barbara
Current Research
# Large scale interactions in financial markets (NSF DMS-2008427)The project is concerned with mathematical understanding of interactions among participants in large financial markets. In order to analyze both homogeneous interaction with the market average and heterogenous interactions with similar participants, graphical interactions are modeled and analyzed with the methods in the system of Stochastic (Partial) Differential Equations (SDEs and SPDEs) with probability distribution constraints. Four problems are considered: 1. Tree structure: extension from the simple, directed chain interaction, 2. Detection problem and beyond: SPDE approach, 3. Model of entangled stochastic volatility in financial markets, 4. Mean-field game and controlled directed chain equation.
In the project the interactions are considered through the pivotal quantities, such as average and ranking, as well as through the local structure of the system. Among various local structures, directed chain and associated system of SDEs with distributional constraints are made in the main focus of the analysis in the first problem. Here, a new class of infinite-dimensional SPDEs emerges in developing the theory of filtering to solve the second problem. As one of applications from the analyses of the first problem, the model of stochastic volatility with directed chain structure is investigated and then the deriving methods are used in the theory of the Mean-field games.
- Tree structure: extension from the simple, directed chain interaction
- Detection problem and beyond: SPDE approach
- Model of entangled stochastic volatility in financial markets
- Mean-field game and controlled directed chain equation
``Linear-Quadratic Stochastic Differential Games on Directed Chain Networks" Journal of Mathematics and Statistical Science (2021) 7 25--67 arXiv: 2003.08840 (with Yichen Feng and Jean-Pierre Fouque).
``Linear-Quadratic Stochastic Differential Games on Random Directed Networks" Journal of Mathematics and Statistical Science (2021) 7 79--108 arXiv:2011.04279 (with Yichen Feng and Jean-Pierre Fouque).
# Information and Stochastic Differential Equations in Financial Markets (NSF DMS-1615229)The proposed project is concerned with mathematical aspects of information flow in financial markets. Based on different aspects in the financial markets three systems of Stochastic Differential Equations (SDEs) are considered. The stochastic analysis on these systems of SDEs is performed with two problems:
- Quantification of Uncertainty in financial portfolios
This part aims to derive various identities and equalities among information sets (filtrations) generated by the sample paths of the stochastic processes which are described by the SDEs with possibly non-smooth coefficients. This part of the project clarifies the difference between the weak solution and the strong solution of the SDEs with more general coefficients.
For it two interesting examples are considered: (i) Walsh diffusions and (ii) Degenerate three particle systems.
In the study of Walsh diffusions we reviewed the (sub-)martingale problem for the Walsh Brownian motion (or Brownian spider or Brownian hedghog), identify teh role of local time for the radial process accumulated at the origin, and extended it to the Walsh diffusion processes; The stationary distribution and convergence to the stationary distribution in the topology of French railway metric. The filtration generated by the Walsh Brownian motion is not generated by Brownian motions because of the behavior of the process in the neighborhood of the origin.
In the study of degenerate three particle systems, we considered the rank-based stochastic differential equations with degeneracy, i.e., the diffusion coefficients are allowed to be zero. This specification opened a number of interesting questions: (a) Does the system of three particles collapse (or triple collision)? (b) If there is a triple collision, how can we describe the system after the triple collisions? The interesting part is that the three particle system after the triple collisions are quite similar to the behaviors of the Walsh Brownian motion in the neighborhood of the origin.
- Trading with additional information in equity markets
This is closely related to an application of Malliavin Calculus and Skorokhod integration in Mathematical Finance. This part is to understand the effects of information asymmetry among traders on portfolio choice.
This insider trader problem is examined in the context of Stochastic Portfolio Theory. We are interested in the (financial) value of information for portfolio investments.
We worked on the relation between a mean-field game model and (a general version of) relative arbitrage over the benchmark, as well as the information drifts. We also considered numerical evaluation of mean-field game equilibria.
This project studies some topics in the system of Stochastic Differential Equations with possibly discontinuous and degenerate diffusion coefficients with applications to stochastic portfolio management and optimization problems. Here the coefficients of the equations are functions of the states and determine the stochastic behavior of the system. The coefficients, the initial states and the stochastic noise of the system are main inputs of the model. The output of the system is the stochastic process which can be construed as the dynamics of the financial system. The long-term goals of the proposed activity are two-folds: (i) to defend against financial crises and (ii) to provide efficient investment strategies in the financial markets.
- Collisions of Brownian particles: Let us consider n tiny Brownian particles which move in the real line and whose dynamics are described by Stochastic Differential Equations with local drifts and local volatility (variance/covariance) coefficients. On the probability space induced by the stochastic differential equations these Brownian particles may collide in the real line. How do these coefficients determine the colliding behaviors of the particles?
- When do three or more particles collide?
- What kind of conditions on the coefficients imply colliding or non-colliding behaviors?
- If they collide, how do they move right after the collision?
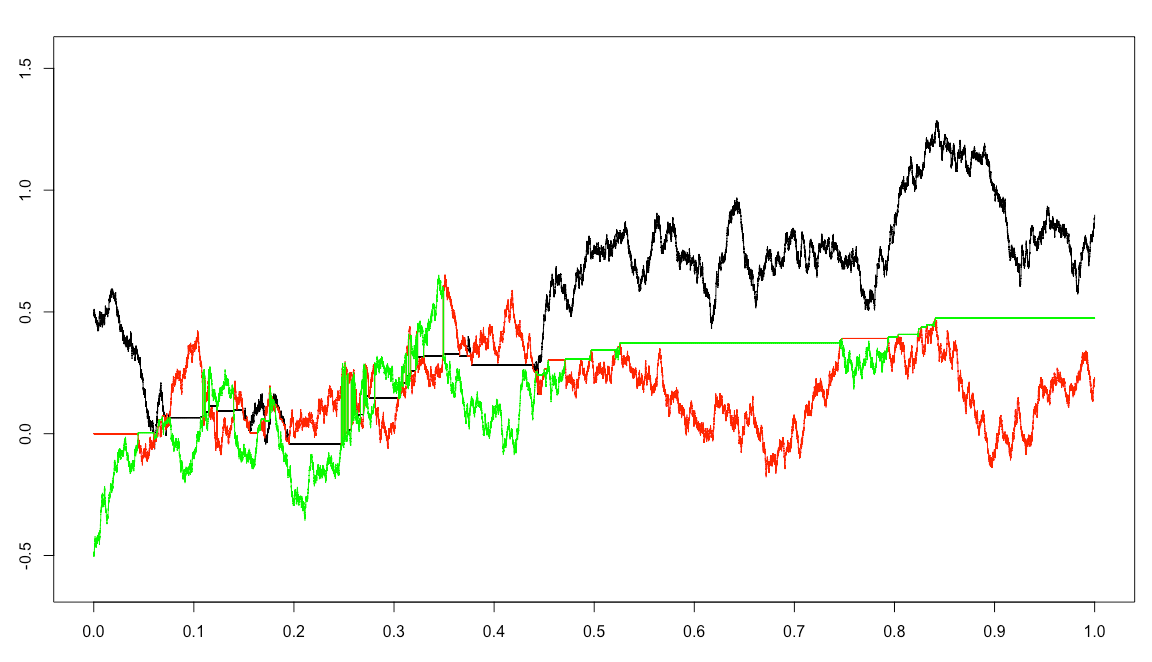
Here is a simulation of the sample path of three interacting particles based on ranks in the real line, where the middle ranked particle behaves ballistically. The horizontal axis is time and the vertical axis is the position of each particle. When three particles (black, green, red) collide, they extricate from the collapse and restart. See the details in ``Degenerate Competing Three-Particle Systems" arXiv: 2006.04970 (with Ioannis Karatzas) to appear in Bernoulli.
- Stochastic Portfolio Theory: The financial equity market has many aspects in its dynamics and stochastic properties. What kind of mathematics can one use in order to understand the market structure? How can our understandings be applied to the better portfolio management? ``Stochastic Portfolio Theory is a novel mathematical framework for analyzing portfolio behavior and equity market structure." [In Preface of Applications of Mathematics Stochastic Modeling and Applied Probability series 48 ``Stochastic Portfolio Theory" (E. Robert Fernholz (2002))]
- Strong/Weak Solutions of Rank-based Continuous Markov Processes: Let us consider n-dimensional stochastic differential equations where the coefficient functions depend on the rankings of the coordinate process corresponding to the equations. Is the system of the stochastic differential equations solvable? If so, in what sense are they solvable, weakly or strongly? This class of diffusions has some interesting behaviors and some applications to Stochastic Portfolio Theory.
- Semimartingale Local Times: The local time process accumulated at a site by a semimartingale measures the intensity of occupation of the semimartingale in the neighborhood of the site. It appears in the above the problems of colliding Brownian motions and the rank-based continuous Markov processes. The main issues are characterization of the local times with various applications.
- Stability and Instability of Interbank-lending: We suffer from the major financial crisis in 2007. In the financial crises flows of money becomes quite important. The flows can be seen as the consequence of various financial activities. What kind of activities can cause the crises? How can one analyze the flows mathematically? Viewing the whole bank activities in an interacting particle system, we analyze the stability and instability of the system.
- Time Reversal: For some class of diffusions it is known that there are some relationship between the forward process and backward process in time. Under some conditions the forward and backward processes match in distribution. We study some applications of time reversal.
Preprints
(1) ``Large deviations for interacting Bessel-like processes and applications to systemic risk" (with M. Shkolnikov) arXiv1303.3061
(2) ``Option pricing with delayed information'' arXiv: 1707.01600 (with Seyyed Mostafa Mousavi).
(3) ``Large Banking Systems with Default and Recovery: A Mean Field Game Model" arXiv: 2001.10206 (with Romuald Elie and Mathieu Lauriere).
(4) ``Relative Arbitrage Opportunities in N Investors and Mean-Field Regimes" arXiv:2006.15158 (with Tianjiao Yang)
(5) ``Semimartingale properties of a generalized fractional Brownian motion and its mixtures with applications in asset pricing" arXiv:2012.00975 (with Guodong Pang and Murad Taqqu) to appear in Finance and Stochastics
(6) ``Optimal investment with insider information using Skorokhod and Russo-Vallois integration" (with Mauricio Elizalde and Carlos Escudero) arXiv:2211.07471
(7) ``Invariant measure of gaps in degenerate competing three-particle systems'' arXiv:2401.10734 (with Sandro Franceschi, Ioannis Karatzas and Killian Raschel, 2024) to appear in Annales de l'Institut Henri Poincare.
(8) ``Stochastic Volterra Integral Equations with Ranks as Scaling Limits of Parallel Infinite-Server Queues under Weighted Shortest Queue Policy'' (with Guodong Pang 2023).
(9) ``Relative arbitrage opportunities in an extended mean-field system'' arXiv: 2311.02690 (with Nicole Tianjiao Yang, 2023).
(10) ``A New Compound Poisson Process and Its Fractional Versions'' (with Palaniappan Vellaisamy) arXiv 2407.18217 2024
(11) ``Rank-based stochastic differential inclusions and diffusion limits for a load balancing model'' (with Rami Atar) arXiv 2409.15121
Recently Published Papers
[25] ``Smoothness of Directed Chain Stochastic Differential Equations" (with Ming Min) Electric Journal of Probability (2024) 29 1-28 arXiv:2202.09354
[24] ``Catalan Numbers, Riccati Equations and Convergence'' (with Yicheng Feng and Jean-Pierre Fouque,) European Journal of Applied Science (2024) 12(4). 407-418. arXiv: 2408.09079
[23] ``Stochastic Analysis of Colliding Brownian Particles'' (in Sugaku, Iwanami Shoten) , 2023 (English Translation will appear in Sugaku Exposition, American Mathematical Society).
[22] ``Systemic Risk Models for Disjoint and Overlapping Groups with Equilibrium Strategies" Statistics and Risk Modeling 40 1-2 (with Y. Feng, J.-P. Fouque and R. Hu) arXiv:2202.00662
[21] ``Degenerate Competing Three-Particle Systems" Bernoulli (2022) 28(3): 2067-2094 arXiv: 2006.04970 (with Ioannis Karatzas)
[20] ``Convolutional Signature for Sequential Data" Digit Finance (2022) arXiv:2009.06719 (with Ming Min).
[19] ``Linear-Quadratic Stochastic Differential Games on Random Directed Networks" Journal of Mathematics and Statistical Science (2021) 7 79--108 arXiv:2011.04279 (with Yichen Feng and Jean-Pierre Fouque).
[18] ``Linear-Quadratic Stochastic Differential Games on Directed Chain Networks" Journal of Mathematics and Statistical Science (2021) 7 25--67 arXiv: 2003.08840 (with Yichen Feng and Jean-Pierre Fouque).
[17] ``Path properties of a generalized fractional Brownian motion" Journal of Theoretical Probability (2021) arXiv: 2009.07788 (with Guodong Pang and Murad Taqqu)
[16] ``Directed chain stochastic differential equation'' Stochastci Processes and their Applications 130 (2020) 2519-2551 arXiv: 1805.01962 (with Nils Detering and Jean-Pierre Fouque)
[15] ``Dynamic Contagion in a Banking System with Births and Defaults'' Annals of Finance (2019) 15 489-538 , arXiv: 1807.09897 (with Michael Ludkovski and Andrey Sarantsev).
[14] ``Stationary distribution and convergence for Walsh diffusions'' Bernoulli Journal Volume 25 (2019) 2439-2478 (with Andrey Sarantsev) arXiv: 1706.07127
[13] ``Stochastic integral equations for Walsh semimartingales" Annales de l'Institut Henri Poincare (2018) Vol. 54, No. 2, 726-756 (with Ioannis Karatzas, Vilmos Prokaj and Minghan Yan) arXiv: 1505.02504
[12] ``Yet another condition for absence of collisions for competing Brownian particles'' Electronic Communications in Probability Volume 22 (2017), paper no. 8, 7 pp. (with Andrey Sarantsev) arXiv:1608.07220
[11] ``Skew-unfolding the Skorokhod reflection of a continuous semimartingale" Stochastic Analysis and Applications 2014 In Honor of Terry Lyons. Springer Proceedings in Mathematics & Statistics (2014) 349-376 (with Ioannis Karatzas) arXiv: 1404.4662.
[10] ``Planar diffusions with rank-based characteristics and perturbed Tanaka equations" Probability Theory and Related Fields 156 (2013) 343-374; a full version with additional topics of Transition probabilities, Time reversibility and Maximality is also available in (with E. R. Fernholz, V. Prokaj and I. Karatzas) arXiv:1108.3992 .
[9] ``Strong solutions of stochastic equations with rank-based coefficients" Probability Theory and Related Fields 156 (2013) 229-248 (with I. Karatzas and M. Shkolnikov) arXiv1109.3823 .
[8] ``Diffusions with rank-based characteristics and values in the nonnegative quadrant" Bernoulli 19 (2013) 2455-2493 (with Ioannis Karatzas and Vilmos Prokaj) arXiv:1202.0036.
[7] ``Convergence rates for rank-based models with applications to portfolio theory" Probability Theory and Related Fields 156 (2013) 415-448 (with S. Pal and M. Shkolnikov) arXiv:1108.0384.
[6] ``A second-order stock market model" Annals of Finance 9 (2013), 439-454 (with R. Fernholz and I. Karatzas) arXiv:1302.3870.
[5] ``Two Brownian particles with rank-based characteristics and skew-elastic collisions'' Stochastic Processes and their Applications 123 (2013) 2999-3026 (with E. Robert Fernholz and Ioannis Karatzas) arXiv:1206.4350 .
[4] ``Stability in a model of inter-bank lending" SIAM Journal of Financial Mathematics 4 (2013) 784-803 (with J-P. Fouque).
[3] ``Hybrid Atlas models" Annals of Applied Probability 21 no 2. (2011), 609-644. (with R. Fernholz, I. Karatzas, A. Banner and V. Papathanakos) arXiv:0909.0065.
[2] ``Collisions of Brownian particles" Annals of Applied Probability 20 no 3. (2010), 951-977 (with I. Karatzas) arXiv:0810.2149.
[1] ``Efficient estimation of one-dimensional diffusion first passage time densities via Monte Carlo simulation" Journal of Applied Probability 48 no 3. (2011) 699-712 (with Constantinos Kardaraz) arXiv:1008.1326.
Dissertation
``Topics in multi-dimensional diffusions: attainability, reflection, ergodicity and rankings'' Dissertation Columbia University. 2009. [924kb].
Conference Proceedings
[C6] ``Directed Chain Generative Adversarial Network" (with Ruimeng Hu and Ming Min) ICML 2023 Proceedings of the 40th Internatinoal Conference on Machine Learning 1033, 24812--24830 arXiv:2304.13131
[C5] ``Smoothness of directed chain stochastic differential equations and its applications" at Probability Symposium Dec. 2022 in RIMS Kokyuroku, Kyoto University, Kyoto, 2023
[C4] ``Stochastic analysis for collision of Brownian particles'' March 2017 The Mathematical Society of Japan.
[C3] ``On mean-field approximation of particle systems with annihilation and spikes'' at Probability Symposium Dec. 2016, published in RIMS RIMS Kokyuroku Kyoto University, Kyoto, 2017.
[C2] `` Folding and Skew-Unfolding of One-dimensional Continuous Semimartingales" RIMS Kokyuroku No 1952: Symposium on Probability Theory, Kyoto 2014
[C1] ``On planar rank-based diffusions with skew-elastic collisions" RIMS Kokyuroku No 1903: Symposium on Probability Theory, Kyoto 2013
Posters
``Degenerate Competing Three Particle Systems" Seminar on Stochatic Processes at Lehigh University (March 2022)
``Detecting Mean-field" Seminar on Stochastic Processes at Brown University (May 2018)
``Stochastic Integral Equations for Walsh Semimartingales" IMA Special Workshop: Reflected Brownian motions, Stochastic Networks and their applications at University of Minnesota (June 2015)
``Strong/Weak Solutions of 2D Diffusions with Rank-based Characterisits" Probabiliy, Control and Finance at Columbia University (May 2012)
Miscellaneous Papers of Statistics in Sports, Biology and Actuarial Science
(S4) ``Estimating the effect of the red card in soccer: when to commit an offense in exchange for preventing a goal opportunity'' Journal of Quantitative Analysis in Sports 5, no. 1 / 2009. (with Jan Vecer and Frantisek Kopriva).
(S3)``On probabilistic excitement of sports games.'' Journal of Quantitative Analysis in Sports 3, no. 6 / 2007. (with Jan Vecer and Mladen Laudanovic).
(S2) ``Assessing substitution variation across sites in grass chloroplast DNA.'' Journal of Molecular Evolution 64, no. 6 pp. 605-613 / June, 2007. (with Tian Zheng and Brian Morton) .
(S1) ``On multi-period statistical risk management methods and equity-linked life insurance.'' Journal of the Japan Statistical Society. Japanese issue 35, no. 2 pp. 103-123. / 2006. abstract. (with Naoto Kunitomo).
Last modified: June 2022.
